What happens if we add another, independent, square root of $-1$? Call it $\ell$. Here we go again.

Cayley and Graves independently discovered the octonions, denoted $\OO$, not long after Hamilton discovered the quaternions. In analogy to the previous construction of $\CC$ and $\HH$, an octonion $x$ can be thought of as a pair of quaternions, $(x_\Hone,x_\Htwo)$, so that \begin{equation} \OO = \HH \oplus \HH \, \ell \end{equation} Since we are running out of letters, we will denote $i$ times $\ell$ simply as $i\ell$, and similarly with $j$ and $k$. But what about the remaining products?

There is a well-defined procedure for producing a new algebra from an old one by adding another copy, known as the Cayley-Dickson process [ 35,15 ]. Elements of the new algebra are pairs $(p,q)$ of elements of the original algebra. The question is, how does one multiply two such elements? The answer turns out to be \begin{equation} (p,q) (r,s) = (pr-\bar{s}q,sp+q\bar{r}) \label{CayleyDixon} \end{equation} If $p,q,r,s\in\RR$, then ($\ref{CayleyDixon}$) is just complex multiplication, with $(p,q)$ identified with $p+qi$. If $p,q,r,s\in\CC$, then ($\ref{CayleyDixon}$) is quaternionic multiplication, with $(p,q)$ identified with $p+qj$. To get the octonionic multiplication table, we simply let $p,q,r,s\in\HH$, and identify $(p,q)$ with $p+q\ell$.

Of course, $\ell^2=-1$; this is built into the construction. It is easy to see that $i\ell$, $j\ell$, and $k\ell$ also square to $-1$; there are now 7 independent imaginary units, and we could write \begin{equation} x = x_1 + x_2 i + x_3 j + x_4 k + x_5 k\ell + x_6 j\ell + x_7 i\ell + x_8 \ell \label{xdef} \end{equation} which can be thought of as a point or vector in $\RR^8$. The real part of $x$ is just $x_1$; the imaginary part of $x$ is everything else. Algebraically, we could define \begin{align} \Re(x) &= \frac12 (x+\bar{x}) \\ \Im(x) &= \frac12 (x-\bar{x}) \end{align} where it is important to note that the imaginary part is, well, imaginary. This differs slightly from the standard usage of these terms for complex numbers, where “$\Im(z)$” normally refers to a real number, the coefficient of $i$. This convention is not possible here, since the imaginary part has 7 degrees of freedom, and can be thought of as a vector in $\RR^7$.

The full multiplication table is summarized in Figure 2. Each point corresponds to an imaginary unit. Each line corresponds to a quaternionic triple, much like $\{i,j,k\}$, with the arrow giving the orientation. For example, \begin{align} k \ell &= k\ell \\ \ell k\ell &= k \\ k\ell k &= \ell \end{align} and each of these products anticommutes, that is, reversing the order contributes a minus sign.

 
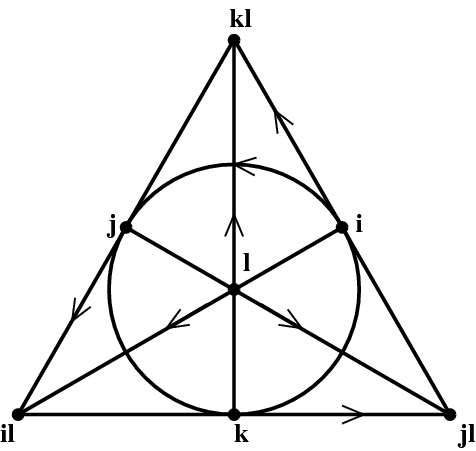
Figure 2: The octonionic multiplication table.

We define the octonionic conjugate $\bar{x}$ of an octonion $x$ as the (real) linear map which reverses the sign of each imaginary unit. Thus, \begin{equation} \bar{x} = x_1 - x_2 i - x_3 j - x_4 k - x_5 k\ell - x_6 j\ell - x_7 i\ell - x_8 \ell \end{equation} if $x$ is given by ($\ref{xdef}$). Direct computation shows that \begin{equation} \bar{xy} = \bar{y}\>\bar{x} \end{equation} The norm of an octonion $|x|$ is defined by \begin{equation} |x|^2 = x\bar{x} = x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 + x_6^2 + x_7^2 + x_8^2 \end{equation} Again, the only octonion with norm $0$ is $0$, and every nonzero octonion has a unique inverse, namely \begin{equation} x^{-1} = {\bar{x} \over  |x|^2} \end{equation} As with the other division algebras, the norm satisfies the identity \begin{equation} |xy| = |x| |y| \label{norm} \end{equation} Writing this out in terms of components yields the 8-squares rule, which is no longer at all obvious. The octonions therefore also form a division algebra.

The Hurwitz Theorem states that $\RR$, $\CC$, $\HH$, and $\OO$ are the only (normed) division algebras (over the real numbers); we can not extend the Cayley-Dickson process any further without obtaining zero divisors. 1)

A remarkable property of the octonions is that they are not associative! For example, compare \begin{align} (i j) (\ell) &= +(k)(\ell)  =  +k\ell \\ (i) (j \ell) &= (i)(j\ell)  =  -k\ell \end{align} However, the octonions are alternative, that is, products involving no more than 2 independent octonions do associate. Specifically, \begin{align} (xy)y &= xy^2 \\ (xy)x &= x(yx) \end{align} for any octonions $x$, $y$. Alternativity extends to products with conjugates, so that \begin{align} (xy)\bar{y} &= x|y|^2 \\ (xy)\bar{x} &= x(y\bar{x}) \end{align}

The commutator (7) of §2. defined for quaternions extends naturally to the octonions as well. We define the associator of three octonions $x$, $y$, $z$ by \begin{equation} [x,y,z] = (xy)z - x(yz) \end{equation} which quantifies the lack of associativity. Alternativity can be phrased as \begin{equation} [x,y,x] = 0 = [x,y,y] \end{equation} More generally, both the commutator and associator are antisymmetric, that is, interchanging any two arguments changes the result by a minus sign; replacing any argument by its conjugate has the same effect, because the real parts don't contribute.

As with the quaternions, the units $i$, $j$, $k$, $k\ell$, $j\ell$, $i\ell$, and $\ell$ are by no means the only square roots of $-1$. Rather, any imaginary octonion squares to a negative number, so it is only necessary to choose its norm to be 1 in order to get a square root of $-1$. The imaginary octonions of norm 1 form a 6-sphere in the 7-dimensional space of imaginary octonions.

Any such unit imaginary octonion $\shat$ can be used to construct a complex subalgebra of $\OO$, which we will also denote by $\CC$, and which takes the form \begin{equation} \CC = \{a + b\,\shat\} \end{equation} with $a,b\in\RR$. We can again use the identity (13) of §1. to write \begin{equation} e^{\shat\theta} = \cos\theta + \shat\sin\theta \end{equation} so that any octonion can be written in the form \begin{equation} x = r e^{\shat\theta} \end{equation} where \begin{equation} r=|x| \end{equation} Two unit imaginary octonions $\shat$ and $\that$ which point in different directions (this excludes $\that=-\shat$) determine a quaternionic subalgebra of $\OO$, which we also denote by $\HH$, and which takes the form \begin{equation} \HH = \{a + b\,\shat + c\,\that + d\,\shat\,\that\,\} \label{Hsub} \end{equation} where $a,b,c,d\in\RR$.

An important technique when working with the octonions is to work with what we call generic octonions. Any single octonion $A$ can be assumed to lie in $\CC$, that is \begin{equation} A = A_1 + A_2 i \end{equation} A second octonion $B$ lies in $\HH$, but adds just one new direction, that is \begin{equation} B = B_1 + B_2 i + B_3 j \end{equation} while a third can be assumed to take the form \begin{equation} C = C_1 + C_2 i + C_3 j + C_4 k + C_8 \ell \end{equation} that is, a general element of $\HH$ plus one further direction. Only with 4 or more octonions is it necessary to use the full 8 dimensions of $\OO$! This approach makes it obvious that any products involving no more than 2 distinct octonions (or their conjugates) must associate — they lie in $\HH$! But this is just alternativity!

It is often useful to consider octonions as vectors in $\RR^8$. The norm of an octonion is precisely the same as its vector norm. But the dot product can be obtained from the norm by a process known as polarization, as follows. If $\vv$, $\ww$ are vectors in $\RR^n$, we have \begin{align} |\vv+\ww|^2 &= (\vv+\ww)\cdot(\vv+\ww) \nonumber\\ &= \vv\cdot\vv + 2\vv\cdot\ww + \ww\cdot\ww \nonumber\\ &= |\vv|^2 + |\ww|^2 + 2\vv\cdot\ww \end{align} which can be solved for the last term. By analogy, the dot product of two octonions is given by \begin{equation} 2 x \cdot y = |x+y|^2 - |x|^2 - |y|^2 = x\bar{y} + y\bar{x} = \bar{x}y + \bar{y}x \end{equation} since $|x|^2=x\bar{x}=\bar{x}x$. For imaginary octonions, orthogonality is equivalent to anticommutativity, that is, \begin{equation} x \cdot y = 0 \Longleftrightarrow x\,y = -y\,x \end{equation} which in turn implies that \begin{equation} \bar{xy} = \bar{y}\>\bar{x} = y\,x = -x\,y \end{equation} so that this is also equivalent to the product being pure imaginary. We can therefore use the dot product to ensure that the product $\shat\,\that$ in ($\ref{Hsub}$) is pure imaginary: If not, simply replace $\that$ by its orthogonal component $\that-(\that\cdot\shat)\,\shat$ (rescaled to have norm 1).

What about the cross product? The cross product of two vectors in $\RR^3$ points in the unique direction (up to sign) orthogonal to the plane spanned by the given vectors. In higher dimensions, there is in general no such preferred direction; there are many directions perpendicular to a given plane. It is therefore somewhat surprising that restricting the octonionic product to imaginary octonions yields a cross product in $\RR^7$ with the usual properties (which are essentially linearity, anticommutativity, and orthogonality to each original vector; there is also a condition on the norm of the cross product). Remarkably, such products exist only in $\RR^3$ and $\RR^7$, corresponding to imaginary quaternions and octonions, respectively.

One way to specify a unique direction in $\RR^n$ is to give $n-1$ directions orthogonal to it. One might therefore suspect that there is a generalized “cross product” in $\RR^n$ involving $n-1$ vectors. This is correct; the resulting product is most easily described in the language of differential forms. But there is precisely one further “generalized cross product” of more than two vectors, namely a product of 3 vectors in $\RR^8$, which also turns out to be related to the octonions. This triple cross product is defined by \begin{equation} x\times y\times z = {1\over2}\Big( x(\bar{y}z)-z(\bar{y}x) \Big) \end{equation} For any octonions $x$, $y$, $z$. (Note that this is not an iterated cross product, but a product directly defined on 3 factors.) The real part of this product defines the associative 3-form $\Phi$, namely \begin{equation} \Phi(x,y,z) = \Re (x \times y \times z) = {1\over2} \, \Re\Big( [x,\bar{y}] z\Big) \end{equation} which we will use later. (The last equality follows by direct computation.)

As with quaternions, a useful strategy for solving problems is to break up the octonions into complex or quaternionic pieces. We have \begin{align} x &= x_\Hone + x_\Htwo \ell \\ &= x_\Cone + x_\Ctwo i + x_\Cthree j + x_\Cfour k \end{align} where $x_\Hone,x_\Htwo\in\HH$ and $x_\Cone,x_\Ctwo,x_\Cthree,x_\Cfour\in\CC$, and where our default conventions are that $\HH$ is the quaternionic subalgebra generated by $i$, $j$, $k$, but $\CC$ is the complex subalgebra determined by $\ell$.

• What is the result of conjugating an octonion by $\ell$?

First of all, there are no associativity issues here since there are only two octonions involved, namely $\ell$ and $x$. The easiest way to work this out is to expand $x$ as in ($\ref{xdef}$), noting that $\ell$ anticommutes with each term except the first and last, so that \begin{equation} \ell y \bar{\ell} = y_1 - y_2 i - y_3 j - y_4 k - y_5 k\ell - y_6 j\ell - y_7 i\ell + y_8 \ell \end{equation} As a special case, for $q\in\HH$ we have \begin{equation} \ell q \bar{\ell} = \bar{q} \label{lcom1} \end{equation} and similarly \begin{equation} \ell (q \ell) \bar{\ell} = \bar{q} \ell \label{lcom2} \end{equation} or equivalently \begin{align} \ell q &= \bar{q} \ell \\ \ell (q \ell) &= -\bar{q} \end{align} These last two expressions are pieces of the Cayley-Dickson multiplication rule ($\ref{CayleyDixon}$), which can be expressed in the form \begin{equation} (x_\Hone + x_\Htwo \ell) (y_\Hone + y_\Htwo \ell) = (x_\Hone y_\Hone - \bar{y_\Htwo} x_\Htwo) + (y_\Htwo x_\Hone + x_\Htwo \bar{y_\Hone}) \ell \end{equation} and from which ($\ref{lcom1}$) and ($\ref{lcom2}$) could have been derived, in the form \begin{equation} \ell (y_\Hone + y_\Htwo \ell) \bar{\ell} = \bar{y_\Hone} + \bar{y_\Htwo} \ell \end{equation}

• What is the result of conjugating an octonion by $e^{\ell\theta}$?

This follows immediately from the similar computation (25) of §2 over the quaternions. Write $x$ in terms of 4 complex numbers as above. Looking first at the quaternionic subalgebra containing $i$ and $\ell$, and then replacing $i$ in turn with $j$ and $k$, leads us to \begin{align} e^{\ell\theta} x e^{-\ell\theta} &= e^{\ell\theta} x_\Cone e^{-\ell\theta} + e^{\ell\theta} x_\Ctwo i e^{-\ell\theta} + e^{\ell\theta} x_\Cthree j e^{-\ell\theta} + e^{\ell\theta} x_\Cfour k e^{-\ell\theta} \nonumber\\ &= x_\Cone + x_\Ctwo e^{2\ell\theta} i + x_\Cthree e^{2\ell\theta} j + x_\Cfour e^{2\ell\theta} k \end{align} As we will see later, this corresponds to a rotation by $2\theta$ in 3 planes at once!