Quaternions
What happens if we add another, independent, square root of $-1$? Call it $j$. Then the big question is, what is $ij$?
Hamilton eventually proposed that $k=ij$ should be yet another square root of $-1$, and that the multiplication table should be cyclic, that is \begin{align} ij = k = -ji \\ jk = i = -kj \\ ki = j = -ik \end{align} We refer to $i$, $j$, and $k$ as imaginary quaternionic units. Notice that these units anticommute!
This multiplication table is shown schematically in Figure 1. Multiplying two of these quaternionic units together in the direction of the arrow yields the third; going against the arrow contributes an additional minus sign.
The quaternions are denoted by $\HH$; the “H” is for Hamilton. 1) They are spanned by the identity element $1$ and three imaginary units, that is, a quaternion $q$ can be thought of as four real numbers ($q_1$,$q_2$,$q_3$,$q_4$), usually written \begin{equation} q = q_1 + q_2 i + q_3 j + q_4 k \label{qdef} \end{equation} which can be thought of as a point or vector in $\RR^4$. Since this can be written in the form \begin{equation} q = (q_1 + q_2i) + (q_3 + q_4i)j \end{equation} we see that a quaternion can be thought of as a pair of complex numbers $(q_\Cone,q_\Ctwo)=(q_1+q_2i,q_3+q_4i)$, or equivalently that we can write \begin{equation} \HH = \CC \oplus \CC j \end{equation} in direct analogy to the construction of $\CC$ from $\RR$.
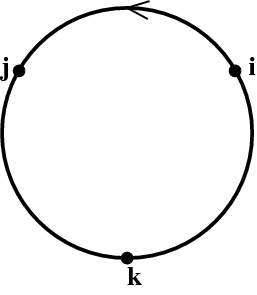
Figure 1: The quaternionic multiplication table.