Freudenthal provided a description of the Lie algebra $\ee_{7(-25)}$, denoted throughout this section simply as $\ee_7$. algebra, [arXiv:1311.0341] . providing a natural symplectic interpretation of its minimal representation. We work throughout with the Lie algebra, but, given our explicit matrix description of $E_{6(-26)}$ in terms of nested operations, it is not difficult to reinterpret our discussion at the group level. In particular, since a Lie algebra is just an infinitesimal representation of a Lie group, both act on the same vector spaces. Our geometric description of the vector space being acted on therefore applies equally well in both cases, even though the objects (nested matrices) acting on it differ.

Let $\XXX,\YYY\in\HHH$ be elements of the Albert algebra, that is, $3\times3$ Hermitian matrices whose components are octonions. As discussed at the group level in § 11.4, the Lie algebra $\ee_{6(-26)}$ (henceforth denoted $\ee_6$) acts on the Albert algebra $\HHH$. The generators of $\ee_6$ fall into one of three categories; there are 26 boosts, 14 derivations (of $\OO$, that is, elements of $\gg_2$), and 38 remaining rotations (the remaining generators of $\ff_4$). For both boosts and rotations, $\phi\in\ee_6$ can be treated as a $3\times3$, tracefree, octonionic matrix; boosts are Hermitian, and rotations are anti-Hermitian. Such matrices $\phi\in\ee_6$ act on the Albert algebra via \begin{equation} \XXX \longmapsto \phi\XXX + \XXX\phi^\dagger \label{e6act} \end{equation} where $\dagger$ denotes conjugate transpose (in $\OO$). 1) As discussed at the group level in § ??, the derivations can be obtained by successive rotations (or boosts) through nesting, corresponding to commutators in the Lie algebra. It therefore suffices to consider the boosts and rotations, that is, to consider matrix transformations. 2)

The dual representation of $\ee_6$ is formed by the duals $\phi'$ of each $\phi\in\ee_6$, defined via \begin{equation} \tr\bigl(\phi(\XXX)\circ \YYY\bigr) = -\tr\bigl(\XXX\circ \phi'(\YYY)\bigr) \end{equation} for $\XXX,\YYY\in\HHH$. It is easily checked that $\phi'=\phi$ on rotations, but that $\phi'=-\phi$ on boosts. Thus, \begin{equation} \phi' = -\phi^\dagger \label{phiadj} \end{equation} for both boosts and rotations.

We can regard $\ee_7$ as the conformal algebra associated with $\ee_6$, since $\ee_7$ consists of the 78 elements of $\ee_6$, together with 27 translations, 27 conformal translations, and a dilation. We follow Freudenthal in representing elements of $\ee_7$ as \begin{equation} \Theta = (\phi,\rho,\AAA,\BBB) \label{ThetaDef} \end{equation} where $\phi\in\ee_6$, $\rho\in\RR$ is the dilation, and $\AAA,\BBB\in\HHH$ are elements of the Albert algebra, representing the translations 3)

What does $\Theta$ act on? We again follow Freudenthal, who describes the elements of the minimal representation of $\ee_7$ in the form \begin{equation} \Pc=(\XXX,\YYY,p,q) \label{Pcdef} \end{equation} where $\XXX,\YYY\in\HHH$, and $p,q\in\RR$. and gives the action of $\Theta$ on $\Pc$ as \begin{align} \XXX &\longmapsto \phi(\XXX) + \frac13\,\rho\,\XXX + 2 \BBB*\YYY + \AAA\,q \label{FreudX}\\ \YYY &\longmapsto 2 \AAA*\XXX + \phi'(\YYY) - \frac13\,\rho\,\YYY + \BBB\,p \label{FreudY}\\ p &\longmapsto \tr(\AAA\circ \YYY) - \rho\,p \label{pFreud}\\ q &\longmapsto \tr(\BBB\circ \XXX) + \rho\,q \label{qFreud} \end{align} But how are we to visualize this action?

The Symplectic Structure of $\so(k+2,2)$

Consider first the analogous problem using $2\times2$ matrices [arXiv:1312.7391] ; see also § . Elements of $\so(k+2,2)$, where $k=|\KK|=1,2,4,8$, can be represented in terms of actions on $4\times4$ matrices of the form \begin{equation} P_0 = \begin{pmatrix} p\,\II & \XX \\ -\tilde\XX & q\,\II \end{pmatrix} \label{P0def} \end{equation} where $\XX$ is a $2\times2$ Hermitian matrix over $\KK$ carrying a representation of $\so(k+1,1)$ (see § 9.3), $p,q\in\RR$, $\II$ denotes the $2\times2$ identity matrix, and tilde denotes trace-reversal, that is, $\tilde\XX=\XX-\tr(\XX)\,\II$. The matrix $P_0$ can be thought of as the upper right $4\times4$ block of an $8\times8$ Clifford algebra representation over $\KK$, and the action of $\so(k+2,2)$ on $P_0$ is obtained as usual from (the restriction of) the quadratic elements of the Clifford algebra. The generators $A\in\so(k+2,2)$ can be chosen so that the action takes the form \begin{equation} P_0 \longmapsto A P_0 \pm P_0 A \label{soact} \end{equation} where the case-dependent signs are related to the restriction from $8\times8$ matrices to $4\times4$ matrices. Following Sudbery, we define the elements $A$ of the symplectic Lie algebra $\sp(4,\KK)$ by the condition 4) \begin{equation} A \Omega + \Omega A^{\dagger} = 0 \label{sp4def} \end{equation} where \begin{equation} \Omega = \begin{pmatrix} \ZeroM& \II\\ -\II& \ZeroM \end{pmatrix} \end{equation} Solutions of (\ref{sp4def}) take the form \begin{equation} A = \begin{pmatrix} \PHI-\frac12\,\rho\,\II& \AA\\ \noalign{\medskip} \BB& -\PHI^\dagger+\frac12\,\rho\,\II \end{pmatrix} \label{Ablock} \end{equation} where both $\AA$ and $\BB$ are Hermitian, $\tr(\PHI)=0$, and $\rho\in\RR$. But generators of \hbox{$\so(k+2,2)$} take exactly the same form: $\PHI$ represents an element of $\so(k+1,1)$, $\AA$ and $\BB$ are (null) translations, and $\rho$ is the dilation. Direct computation shows that the generators $A$ of \hbox{$\so(k+2,2)$} do indeed satisfy (\ref{sp4def}), so that $\so(k+2,2)$ and $\sp(4,\KK)$ can be identified as vector spaces, and hence also as Lie algebras; the above construction therefore establishes the isomorphism \begin{equation} \so(k+2,2) \cong \sp(4,\KK) \end{equation}

We can bring the representation (\ref{P0def}) into a more explicitly symplectic form by treating $\XX$ as a vector-valued 1-form, and computing its Hodge dual ${*}\XX$, defined by \begin{equation} {*}\XX = \XX\EPS \end{equation} where \begin{equation} \EPS = \begin{pmatrix} 0& 1\\ -1& 0 \end{pmatrix} \end{equation} is the Levi-Civita tensor in two dimensions. Using the identity \begin{equation} \EPS \XX \EPS = \tilde\XX{}^T \end{equation} we see that $P=P_0\,\II\otimes\EPS$ takes the form \begin{equation} P = \begin{pmatrix} p\,\EPS& {*}\XX\\ -({*}\XX)^T& q\,\EPS \end{pmatrix} \label{Squarie} \end{equation}

Figure 1a: The block structure of a $4\times4$ antisymmetric matrix in terms of $2\times2$ blocks. A binary labeling of the blocks is shown above.

Figure 1b: As above; blocks with similar shading contain equivalent information.

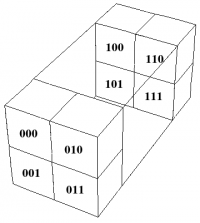
which is antisymmetric, and whose block structure is shown in Figure 1. The diagonal blocks, labeled $00$ and $11$, are antisymmetric, and correspond to $p$ and $q$, respectively, whereas the off-diagonal blocks, labeled $01$ and $10$, contain equivalent information, corresponding to ${*}\XX$. Note that ${*}\XX$ does not use up all of the degrees of freedom available in an off-diagonal block; the set of all antisymmetric $4\times4$ matrices is not an irreducible representation of $\sp(4,\KK)$.

The action of $\sp(4,\KK)$ on $P$ is given by \begin{equation} P \longmapsto AP + PA^T \label{sp4act} \end{equation} for $A\in\sp(4,\KK)$, that is, for $A$ satisfying (\ref{sp4def}). 5) When working over $\KK=\RR$ or $\CC$, the action (\ref{sp4act}) is just the antisymmetric square \begin{equation} v \wedge w \longmapsto Av \wedge w + v \wedge Aw \label{wedge2} \end{equation} of the natural representation $v\longmapsto Av$, with $v\in\KK^4$.

Cubies

Before generalizing the above construction to the $3\times3$ case, we first consider the analog of ${*}\XX$. Let $\XXX\in\HHH$ be an element of the Albert algebra, which we can regard as a vector-valued 1-form with components $\XXX_a{}^b$, with $a,b\in\{1,2,3\}$. The Hodge dual ${*}\XXX$ of $\XXX$ is a vector-valued 2-form with components \begin{equation} (*\XXX)_{abc}=\XXX_a{}^m\epsilon_{mbc} \label{Hodge} \end{equation} where $\epsilon_{abc}$ denotes the Levi-Civita tensor in three dimensions, that is, the completely antisymmetric tensor satisfying \begin{equation} \epsilon_{123} =1 \end{equation} and where repeated indices are summed over. We refer to ${*}\XXX$ as a cubie. We also introduce the dual of $\epsilon_{abc}$, the completely antisymmetric tensor $\epsilon^{abc}$ satisfying \begin{equation} \epsilon_{mns}\epsilon^{mns} = 6 \label{eps6} \end{equation} and note the further identities \begin{align} \epsilon_{amn}\,\epsilon^{bmn} &= 2\,\delta_a{}^b \\ \epsilon_{abm}\,\epsilon^{cdm} &= \delta_a{}^c \,\delta_b{}^d - \delta_a{}^d \,\delta_b{}^c \\ \epsilon_{abc}\,\epsilon^{def} &= \delta_a{}^d\,\delta_b{}^e\,\delta_c{}^f + \delta_b{}^d\,\delta_c{}^e\,\delta_a{}^f + \delta_c{}^d\,\delta_a{}^e\,\delta_b{}^f \nonumber\\ &\qquad - \delta_a{}^d\,\delta_c{}^e\,\delta_b{}^f - \delta_b{}^d\,\delta_a{}^e\,\delta_c{}^f - \delta_c{}^d\,\delta_a{}^e\,\delta_b{}^f \label{epssq} \end{align} In particular, we have \begin{equation} ({*}\XXX)_{amn}\epsilon^{bmn} = 2 \XXX_a{}^b \label{sinv} \end{equation}

Operations on the Albert algebra can be rewritten in terms of cubies. For instance, \begin{align} \tr\XXX &= \frac12\, \XXX_{abc} \,\epsilon^{abc} \\ \bigl({*}(\XXX\,\YYY)\bigr)_{abc} &= \frac12\, \XXX_{amn}\,\YYY_{pbc} \,\epsilon^{mnp} \\ \bigl({*}(\XXX\circ\YYY)\bigr)_{abc} &= \frac14 \bigl( \XXX_{amn}\,\YYY_{pbc} + \YYY_{amn}\,\XXX_{pbc} \bigr) \,\epsilon^{mnp} \\ \tr(\XXX\circ\YYY) &= \frac18 \bigl( \XXX_{amn}\,\YYY_{pbc} + \YYY_{amn}\,\XXX_{pbc} \bigr) \,\epsilon^{mnp}\,\epsilon^{bca} \nonumber\\ &= \frac18 \bigl( \XXX_{amn}\,\YYY_{pbc} + \YYY_{pbc}\,\XXX_{amn} \bigr) \,\epsilon^{mnp}\,\epsilon^{bca} \\ (\tr\XXX)(\tr\YYY) &= \frac12\, \XXX_{abc}\,\YYY_{def} \,\epsilon^{abc}\,\epsilon^{def} \end{align} from which the components of ${*}(\XXX*\YYY)$ can also be worked out. In the special case where the components of $\XXX$ and $\YYY$ commute, contracting both sides of (\ref{epssq}) with $\XXX\otimes\YYY$ yields \begin{equation} \frac12 \XXX_c{}^m \YYY_d{}^n \,\epsilon_{amn} \,\epsilon^{bcd} = (\XXX*\YYY)_a{}^b \label{cFreud} \end{equation} or equivalently \begin{equation} \bigl({*}(\XXX*\YYY)\bigr)_{abc} = \frac12 (\XXX_b{}^m \YYY_c{}^n - \XXX_c{}^m \YYY_b{}^n) \,\epsilon_{amn} \end{equation} providing two remarkably simple expressions for the Freudenthal product, albeit only in a very special case. We will return to this issue below.

The Symplectic Structure of $\ee_7$

Figure 2a: The block structure of a $6\times6\times6$ antisymmetric tensor in terms of $3\times3\times3$ “cubies”. A binary labeling of the cubies is shown on the pulled-apart cube above.

Figure 2b: As above; cubies with similar shading contain equivalent information.

The representation (\ref{ThetaDef}) can be written in block form, which we also call $\Theta$, namely 6) \begin{equation} \Theta = \begin{pmatrix} \phi-\frac13\,\rho\,\III& \AAA\\ \noalign{\medskip} \BBB& \phi'+\frac13\,\rho\,\III \label{e7mat} \end{pmatrix} \end{equation} where $\III$ denotes the $3\times3$ identity matrix. By analogy with Section \ref{sp4}, we would like $\Theta$ to act on ${*}\XXX$, which has 3 indices, and is antisymmetric in 2 of them, and hence has the correct symmetries to be an off-diagonal block of a rank 3 antisymmetric tensor $\Pc$. The components of $\Pc$ make up a $6\times6\times6$ cube, which we divide into $3\times3\times3$ cubies, as shown in Figure 2; compare Figure 1. We identity the diagonal cubies, labeled $000$ and $111$, with $p\,{*}\III$ and $q\,{*}\III$, respectively, the cubie labeled $011$ with ${*}\XXX$, the cubie labeled $100$ with ${*}\YYY$, and then let antisymmetry do the rest. Explicitly, we have \begin{equation} \Pc_{abc} = \begin{cases} p\, \epsilon_{abc} & a\le3,b\le3,c\le3 \\ ({*}\YYY)_{\hat{a}bc} & a\ge4,b\le3,c\le3 \\ ({*}\XXX)_{a\hat{b}\hat{c}} & a\le3,b\ge4,c\ge4 \\ q\, \epsilon_{\hat{a}\hat{b}\hat{c}} & a\ge4,b\ge4,c\ge4 \end{cases} \label{Pblocks} \end{equation} where we have introduced the convention that $\hat{a}=a-3$, and where the remaining components are determined by antisymmetry. 7)

In the complex case, we could begin with the natural action of $\Theta$ on 6-component complex vectors, and then take the antisymmetric cube, that is, we could consider the action \begin{equation} u\wedge v \wedge w \longmapsto \Theta u \wedge v \wedge w + u\wedge \Theta v \wedge w + u\wedge v \wedge \Theta w \label{wedge3} \end{equation} with $u,v,w\in\CC^6$, or equivalently \begin{equation} \Pc_{abc} \longmapsto \Theta_a{}^m \Pc_{mbc} + \Theta_b{}^m \Pc_{amc} + \Theta_c{}^m \Pc_{abm} \label{Pact} \end{equation} Over the octonions, however, the action (\ref{Pact}) must be modified and reinterpreted in order to yield the Freudenthal action (\ref{FreudX}). We summarize the resulting description below; see [arXiv:1311.0341] for further details.

The basic idea is to reorder (\ref{Pact}), using instead the action \begin{equation} \Pc_{abc} \longmapsto \Theta_a{}^m \Pc_{mbc} + \Pc_{amc} \Theta_b{}^m + \Pc_{abm} \Theta_c{}^m \label{cubeact} \end{equation} which, however, is only antisymmetric in its last two indices. We therefore use (\ref{cubeact}) to define the action only on cubies $000$, $011$, $100$, and $111$; the action on the remaining 4 cubies is uniquely determined by requiring that antisymmetry be preserved. This approach succeeds, thanks to the following results [arXiv:1311.0341] , which we state without proof

Lemma: The action of the dilation $\Theta=(0,\rho,0,0)\in\ee_7$ on $\Pc$ is given by (\ref{Pact}). \label{dilemma}

Lemma: If the elements of $\AAA,\BBB\in\HHH$ commute with those of $\Pc$, then the action of the translations $\Theta=(0,0,\AAA,0)$ and $\Theta=(0,0,0,\BBB)$ on $\Pc$ is given by (\ref{Pact}). \label{trlemma}

Over $\RR$ or $\CC$, we're done; Lemmas \ref{e6lemma}, \ref{dilemma}, and \ref{trlemma} together suffice to show that the action (\ref{Pact}) is the same as the Freudenthal action (\ref{FreudX})–(\ref{qFreud}). Unfortunately, the action (\ref{Pact}) fails to satisfy the Jacobi identity over $\HH$ or $\OO$. However, we can still use Lemmas \ref{e6lemma}, \ref{dilemma}, and \ref{trlemma} to reproduce the Freudenthal action in those cases, as follows.

Lemma: The action of $\phi\in\ee_6$ on cubies is given by \begin{equation} ({*}\XXX)_{abc} \longmapsto \phi_a{}^m ({*}\XXX)_{mbc} + ({*}\XXX)_{amc} \phi'_b{}^m + ({*}\XXX)_{abm} \phi'_c{}^m \label{e6cact} \end{equation} \label{e6lemma}

Lemma: The action of $\Theta=(\phi,0,0,0)\in\ee_7$ on $\Pc$ is determined by (\ref{cubeact}) when acting on elements of the form (\ref{Pblocks}), which extends to all of $\ee_7$ by antisymmetry. \label{e6lemma2}

Putting these pieces together, we obtain the final result.

Theorem: The Lie algebra $\ee_7$ acts symplectically on cubes, that is, $\ee_6\subset\ee_7$ acts on cubes via (\ref{cubeact}), as do real translations and the dilation, and all other $\ee_7$ transformations can then be constructed from these transformations using linear combinations and commutators. \label{Thm}

Proof: Lemmas \ref{dilemma} and \ref{trlemma} are unchanged by the use of (\ref{cubeact}) rather than (\ref{Pact}), since the components of $\Theta$ commute with those of $\Pc$ in both cases, and Lemma \ref{e6lemma2} verifies that $\ee_6$ acts via (\ref{cubeact}), as claimed. It only remains to show that the remaining generators of $\ee_7$ can be obtained from these elements via commutators.

Using (\ref{FreudX})–(\ref{qFreud}), it is straightforward to compute the commutator of two $\ee_7$ transformations of the form (\ref{ThetaDef}). Letting $\phi=\Qcal\in\ee_6$ be a boost, so that $\Qcal^\dagger=\Qcal$ and $\tr(\Qcal)=0$, and using the identity \begin{equation} -(\AAA\circ\BBB)*\XXX = \bigl(\BBB-\tr(\BBB)\III\bigr)\circ(\AAA*\XXX) + \AAA*(\BBB\circ\XXX) \end{equation} for any $\AAA,\BBB,\XXX\in\HHH$, we obtain \begin{equation} \bigl[(0,0,\AAA,0),(\Qcal,0,0,0)\bigr] = (0,0,\AAA\circ\Qcal,0) \end{equation} We can therefore obtain the null translation $(0,0,\Qcal,0)$ for any tracefree Albert algebra element $\Qcal$ as the commutator of $(0,0,\III,0)$ and $(\Qcal,0,0,0)$; a similar argument can be used to construct the null translation $(0,0,0,\Qcal)$.

Thus, all generators of $\ee_7$ can be implemented either as a symplectic transformation on cubes via (\ref{cubeact}), or as the commutator of two such transformations.

Further Properties

We have showed that the algebraic description of the minimal representation of $e_7$ introduced by Freudenthal corresponds geometrically to a symplectic structure. Along the way, we have emphasized both the similarities and differences between $\ee_7$ and $\so(10,2)$. Both of these algebras are conformal; their elements divide naturally into generalized rotations ($\ee_6$ or $\so(9,1)$, respectively), translations, and a dilation. Both act naturally on a representation built out of vectors ($3\times3$ or $2\times2$ Hermitian octonionic matrices, respectively), together with two additional real degrees of freedom ($p$ and $q$). In the $2\times2$ case, the representation (\ref{P0def}) contains just one vector; in the $3\times3$ case (\ref{Pcdef}), there are two. This at first puzzling difference is fully explained by expressing both representations as antisymmetric tensors, as in (\ref{Squarie}) and (\ref{Pblocks}), respectively, and as shown geometrically in Figures 1 and 2.

In the complex case, we have shown that the symplectic action (\ref{Pact}) exactly reproduces the Freudenthal action (\ref{FreudX})–(\ref{qFreud}). The analogy goes even further. In $2n$ dimensions, there is a natural map taking two $n$-forms to a tensor of rank $2$. When acting on $\Pc$ (so $n=3$), this map takes the form \begin{equation} \Pc \longmapsto \Pc_{acd}\Pc_{efg}\,\epsilon^{cdefgb} \label{PstarP} \end{equation} where $\epsilon$ now denotes the volume element in six dimensions, that is, the completely antisymmetric tensor with $\epsilon^{123456}=1$. Freudenthal also gives us a “squaring” operation on $\ee_7$, namely the “super-Freudenthal” product $*$ taking elements $\Pc$ of the minimal representation of $\ee_7$ to elements of $\ee_7$, given by 8) \begin{equation} \Pc*\Pc = (\phi,\rho,\AAA,\BBB) \label{PstarP0} \end{equation} where \begin{align} \phi &= \langle \XXX,\YYY\rangle \label{PstarP1}\\ \rho &= -\frac14 \tr\bigl(\XXX\circ\YYY - pq\,\III\bigr) \\ \AAA &= -\frac12 \bigl(\YYY*\YYY - p\,\XXX\bigr) \\ \BBB &= \frac12 \bigl(\XXX*\XXX - q\,\YYY\bigr) \label{PstarP4} \end{align} and where \begin{align} \langle X,Y\rangle Z &= Y\circ(X\circ Z) - X\circ(Y\circ Z) \nonumber\\ &\qquad - (X\circ Y)\circ Z + \frac13 \tr(X\circ Y) Z \end{align} It is not hard to verify that, in the complex case, (\ref{PstarP}) is (a multiple of) $\Pc*\Pc$, as given by (\ref{PstarP0})–(\ref{PstarP4}).

Furthermore, $\ee_7$ preserves the quartic invariant \begin{align} J &= \tr\bigl( (\XXX*\XXX)\circ(\YYY*\YYY) \bigr) - p\det\XXX - q\det\YYY \nonumber\\ &\qquad\qquad -\frac14 \bigl( \tr(\XXX\circ\YYY)-pq \bigr)^2 \label{quartic} \end{align} which can be constructed using $\Pc*\Pc$. Not surprisingly, the quartic invariant (\ref{quartic}) can be expressed in the complex case as \begin{equation} J \sim \Pc_{gab}\Pc_{cde}\Pc_{fhi}\Pc_{jkl} \,\epsilon^{abcdef}\,\epsilon^{ghijkl} \label{quarticC} \end{equation} up to an overall factor.

Neither the form of the action (\ref{Pact}), nor the expressions (\ref{PstarP}) and (\ref{quarticC}), hold over $\HH$ or $\OO$. This failure should not be a surprise, as trilinear tensor products are not well defined over $\HH$, let alone $\OO$. Nonetheless, Theorem \ref{Thm} does tell us how to extend (\ref{Pact}) to the octonions. Although it is also possible to write down versions of (\ref{PstarP}) and (\ref{quarticC}) that hold over the octonions, by using case-dependent algorithms to determine the order of multiplication, it is not clear that such expressions have any advantage over the original expressions (\ref{PstarP0})–(\ref{PstarP4}) and (\ref{quartic}) given by Freudenthal.

Despite these drawbacks, it is clear from our construction that $\ee_{7(-25)}$ should be regarded as a natural generalization of the traditional notion of a symplectic Lie algebra, and fully deserves the name $\sp(6,\OO)$. Furthermore, given our construction of $E_6$ in terms of nested matrices acting on the Albert algebra, it is not difficult to extend the treatment given here from the Lie algebra $\ee_7$ to the Lie group $E_7$, thus showing how $E_7$ acts on cubies, and justifying the identification $E_7\cong\Sp(6,\OO)$.