You are here: start » book » go2 » quaternionsn
Quaternions
What happens if we add another, independent, square root of $-1$? Call it $j$. Then the big question is, what is $ij$?
Hamilton eventually proposed that $k:=ij$ should be yet another square root of $-1$, and that the multiplication table should be cyclic, that is \begin{align} ij = k = -ji \\ jk = i = -kj \\ ki = j = -ik \end{align} We refer to $i$, $j$, and $k$ as imaginary quaternionic units. Notice that these units anticommute!
This multiplication table is shown schematically in Figure 1. Multiplying two of these quaternionic units together in the direction of the arrow yields the third; going against the arrow contributes an additional minus sign.
The quaternions are denoted by $\HH$; the “H” is for Hamilton. They are spanned by the identity element $1$ and three imaginary units, that is, a quaternion $q$ can be thought of as four real numbers ($q_1$,$q_2$,$q_3$,$q_4$), usually written \begin{equation} q = q_1 + q_2 i + q_3 j + q_4 k \label{qdef} \end{equation} which can be thought of as a point or vector in $\RR^4$. Since this can be written in the form \begin{equation} q = (q_1 + q_2i) + (q_3 + q_4i)j \end{equation} we see that a quaternion can be thought of as a pair of complex numbers $(q_\Cone,q_\Ctwo)=(q_1+q_2i,q_3+q_4i)$, or equivalently that we can write \begin{equation} \HH = \CC \oplus \CC j \end{equation} in direct analogy to the construction of $\CC$ from $\RR$.
The quaternionic multiplication table is almost, but not quite, the vector cross product. The only difference is that imaginary quaternions square to a negative number, whereas the cross product of a vector with itself is zero.
This is not a coincidence. Making the obvious identification of vectors $\vv$, $\ww$ with imaginary quaternions $v$, $w$, then the imaginary part of the quaternionic product $vw$ is the cross product $\vv\times\ww$, while the real part is just (minus) the dot product $\vv\cdot\ww$! In fact, the use of $\,\ii$, $\jj$, $\kk$ for Cartesian basis vectors originates with the quaternions, which predate the use of vectors [ 8 ].
We define the commutator of two quaternions $p$ and $q$ by \begin{equation} [p,q] = pq - qp \label{commutator} \end{equation} which quantifies the lack of commutativity of the quaternions. For example, we have $[i,j]=2k$. However, the quaternions are associative; it is sufficient to check that \begin{equation} (ij)k = -1 = i(jk) \end{equation} And we assume distributivity of multiplication over addition.
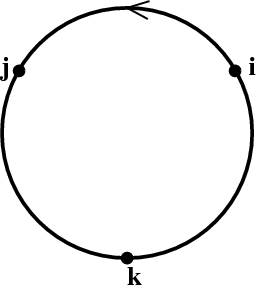
Figure 1: The quaternionic multiplication table.
We define the quaternionic conjugate $\bar{q}$ of a quaternion $q$ as the (real) linear map which reverses the sign of each imaginary unit. Thus, \begin{equation} \bar{q} = q_1 - q_2 i - q_3 j - q_4 k \end{equation} if $q$ is given by ($\ref{qdef}$). This leads directly to the norm of a quaternion $|q|$, defined by \begin{equation} |q|^2 = q\bar{q} = q_1^2 + q_2^2 + q_3^2 + q_4^2 \end{equation} Again, the only quaternion with norm $0$ is $0$, and every nonzero quaternion has a unique inverse, namely \begin{equation} q^{-1} = {\bar{q} \over |q|^2} \end{equation}
Quaternionic conjugation satisfies the identity \begin{equation} \bar{pq} = \bar{q}\>\bar{p} \end{equation} from which it follows that the norm satisfies: \begin{equation} |pq| = |p| |q| \end{equation} Writing this out in terms of components yields the 4-squares rule, which is not quite as obvious as the 2-squares rule. Note that this identity means that the quaternions form a division algebra. That is, not only are there inverses, but there are no zero divisors — if a product is zero, one of the factors must be zero.
It is important to realize that $\pm i$, $\pm j$, and $\pm k$ are not the only square roots of $-1$. Rather, any imaginary quaternion squares to a negative number, so it is only necessary to choose its norm to be 1 in order to get a square root of $-1$. The imaginary quaternions of norm 1 form a sphere; in the above notation, this is the set of points \begin{equation} q_2^2 + q_3^2 + q_4^2 = 1 \end{equation} (and $q_1=0$). Any such unit imaginary quaternion $\shat$ can be used to construct a complex subalgebra of $\HH$, which we will also denote by $\CC$, namely \begin{equation} \CC = \{a + b\,\shat\} \end{equation} with $a,b\in\RR$. Furthermore, we can use the identity (13) of §1. to write \begin{equation} e^{\shat\theta} = \cos\theta + \shat\sin\theta \end{equation} This means that any quaternion can be written in the form \begin{equation} q = r e^{\shat\theta} \end{equation} where \begin{equation} r=|q| \end{equation}
Since quaternions are invertible, linear equations such as (9) of §1, where now $x,y,z\in\HH$, can still be solved for $z$ so long as $x\ne0$. But these are no longer the only linear equations! Consider for instance the equation \begin{equation} d = a x + x b \end{equation} where now $a,b,d\in\CC$ and $x\in\HH$. One solution is clearly \begin{equation} x_0 = {d\over a+b} \label{csol} \end{equation} provided $a+b\ne0$. Note that $x_0$ is complex. Are there any other solutions? Consider the special case $d=0$, $a=i=b$. Then any linear combination of $j$ and $k$ solves the equation!
This turns out to be the generic situation: If $a+\bar{b}\ne0$, then the only solution is the complex solution ($\ref{csol}$), but if $a+\bar{b}=0$ there are additional quaternionic “homogeneous” solutions, which can be added to the particular solution $x_0$, which is therefore not unique. The situation rapidly becomes more complicated if some or all of $a$, $b$, $d$ are themselves allowed to be quaternionic, rather than complex.
A useful strategy for solving problems such as the one above, which involve both complex numbers and quaternions, is to break up the quaternions into a pair of complex numbers. Consider the following examples.
We define conjugation of one quaternion $q$ by another quaternion $p$ is defined by $pqp^{-1}$. Note that the norm of $p$ is irrelevant here, so we might as well assume that $|p|=1$, in which case $p^{-1}=\bar{p}$
- What is the result of conjugating a quaternion by $i$?
Write $q$ in terms of a pair of complex numbers via \begin{equation} q = q_\Cone + q_\Ctwo j \end{equation} Then $i$ commutes with the complex numbers $q_\Cone$ and $q_\Ctwo$, but anticommutes with $j$. Thus, \begin{equation} iq\bar\imath = i q_\Cone \bar\imath + i q_\Ctwo j \bar\imath = i q_\Cone \bar\imath - i q_\Ctwo \bar\imath j = q_\Cone - q_\Ctwo j \end{equation} Conjugation by $i$ therefore leaves the complex plane untouched, but yields a reflection in the $jk$-plane. Analogous results would hold for conjugation by any other imaginary quaternionic unit, such as $\shat$.
- What is the result of conjugating a quaternion by $e^{i\theta}$?
Note first of all that, interchanging the roles of $i$ and $j$ in the previous discussion, conjugation by $j$ yields a reflection in the $ki$-plane, so that \begin{equation} j e^{-i\theta} \bar\jmath = e^{i\theta} \end{equation} Multiplying both of these equations on the right by $j$ yields the important relation \begin{equation} j e^{-i\theta} = e^{i\theta} j \end{equation} Thus, \begin{align} e^{i\theta} q e^{-i\theta} &= e^{i\theta} q_\Cone e^{-i\theta} + e^{i\theta} q_\Ctwo j e^{-i\theta} \nonumber\\ &= e^{i\theta} q_\Cone e^{-i\theta} + e^{i\theta} q_\Ctwo e^{i\theta} j \nonumber\\ &= q_\Cone + q_\Ctwo e^{2i\theta} j \label{Hrot} \end{align} As we will see later, this corresponds to a rotation by $2\theta$ in the $jk$-plane.