The description in the preceding chapters of 10-dimensional Minkowski space in terms of Hermitian octonionic matrices is a direct generalization of the usual description of ordinary (4-dimensional) Minkowski space in terms of complex Hermitian matrices. If we fix a complex subalgebra $\CC\subset\OO$, then we single out a 4-dimensional Minkowski subspace of 10-dimensional Minkowski space. The projection of a 10-dimensional null vector onto this subspace is a causal 4-dimensional vector, which is null if and only if the original vector was already contained in the subspace, and timelike otherwise. The time orientation of the projected vector is the same as that of the original, and the induced mass is given by the norm of the remaining 6 components. Furthermore, the ordinary Lorentz group $SO(3,1)$ clearly sits inside the Lorentz group $SO(9,1)$ via the identification of their double-covers, the spin groups $\hbox{Spin}(d,1)$, namely \begin{equation} \hbox{Spin}(3,1) = SL(2,\CC) \subset SL(2,\OO) = \hbox{Spin}(9,1) \end{equation}

Therefore, all it takes to break 10 spacetime dimensions to 4 is to choose a preferred octonionic unit to play the role of the complex unit. We choose $\ell$ rather than $i$ to fill this role, preferring to save $i$, $j$, $k$ for a (distinguished) quaternionic triple. The projection $\pi$ from $\OO$ to $\CC$ is given by \begin{equation} \pi(q) = {1\over2} (q + \ell q \bar\ell) \end{equation} and we thus obtain a preferred $SL(2,\CC)$ subgroup of $SL(2,\OO)$, corresponding to the “physical” Lorentz group.

For each solution $\psi$ of (1) of §14, the momentum is proportional to $\psi\psi^\dagger$ by (4) of §14. Up to an overall factor, we can therefore read off the components of the 4-dimensional momentum $p^\mu$ directly from $\pi(\psi\psi^\dagger)$. Note that the projection of a 10-dimensional lightlike vector to 4 dimensions results in a causal vector, that is, in a vector which is either lightlike or timelike. In other words, the resulting 4-momentum is that of a massless or massive particle, respectively. We can use a (4-dimensional!)\ Lorentz transformation to bring a massive particle to rest, or to orient the momentum of a massless particle to be in the $z$-direction.

As in the previous chapter, we will assume that the components of $\Psi$ — and hence also $\PPP$ — lie in the quaternionic subalgebra containing $k$ and $\ell$, and that $p^{k\ell}=0$. We therefore have \begin{equation} \PPP = \pi(\PPP) + m\SIGMA_k \end{equation} which shows explicitly the relationship between the higher-dimensional lightlike vector $\PPP$, the causal 4-dimensional vector $\pi(\PPP)$, and the mass $m$.

If $m\ne0$, we can distinguish particles from antiparticles by the sign of the term involving $m$, which is the coefficient of $\SIGMA_k$ in $\PPP$. Equivalently, we have the particle/antiparticle projections (at rest) \begin{equation} \PI_\pm = {1\over2} \left( \II \pm \SIGMA_k \right) \end{equation} If $m=0$, however, we can only distinguish particles from antiparticles in momentum space by the sign of $p^t$, as usual; this is the same as the sign in (4) of §14. Similarly, in this language, the chiral projection operator is constructed from \begin{equation} \UPSILON_5 = \SIGMA_t \SIGMA_x \SIGMA_y \SIGMA_z = - \begin{pmatrix}\ell& 0\cr 0& \ell\cr\end{pmatrix} \end{equation} However, as with spin, we must multiply by $\ell$ in the correct place, that is \begin{equation} \hat\UPSILON_5 [\psi] = \UPSILON_5 \psi \ell \end{equation} As a result, even though $\UPSILON_5$ is a multiple of the identity, $\hat\UPSILON_5$ is not, and the operators ${1\over2}(\II\pm\hat\UPSILON_5)$ project $\HH^2$ into the Weyl subspaces $\CC^2\oplus\CC^2 k$ as desired.

Combining the spin and particle information, over the quaternionic subalgebra $\HH\subset\OO$ determined by $k$ and $\ell$, we thus find 1 massive spin-${1\over2}$ particle at rest, with 2 spin states, namely \begin{equation} \eplus = \begin{pmatrix}1\cr k\cr\end{pmatrix} \qquad \eminus = \begin{pmatrix}-k\cr   1\cr\end{pmatrix} \end{equation} Both of these spinors (of course) have the same momentum, namely \begin{equation} \eplus\phd \eplus^\dagger = \eminus\phd \eminus^\dagger = \begin{pmatrix}1&-k\cr k&  1\cr\end{pmatrix} \end{equation} corresponding to a particle at rest (with $m=1$). The corresponding antiparticles are obtained by replacing $k$ by $-k$ (and changing the sign in (4) of §14.

We also find 1 massless spin-${1\over2}$ particle involving $k$, namely \begin{equation} \nu_z = \begin{pmatrix}0\cr k\cr\end{pmatrix} \end{equation} whose momentum is \begin{equation} \nu_z\phd \nu_z^\dagger = \begin{pmatrix}0&0\cr 0&1\cr\end{pmatrix} \end{equation} and which is therefore moving at the speed of light in the $z$-direction. This corresponds, as usual, to both a particle and its antiparticle. It is important to note that \begin{equation} \numz = \begin{pmatrix}k\cr 0\cr\end{pmatrix} \end{equation} has momentum \begin{equation} \numz\phd \numz^\dagger = \begin{pmatrix}1&0\cr 0&0\cr\end{pmatrix} \end{equation} and thus corresponds to a massless particle with the same helicity moving in the opposite direction, not to a different particle with the opposite helicity.

Each of the above states may be multiplied (on the right) by an arbitrary complex number without affecting its properties.

So far we have 1 massive particle with 2 helicity states, and 1 massless particle with a single helicity state. These are precisely the observed mass and helicity properties of a generation of leptons! We therefore interpret $e$ as an electron, and $\nu$ as a neutrino.

 
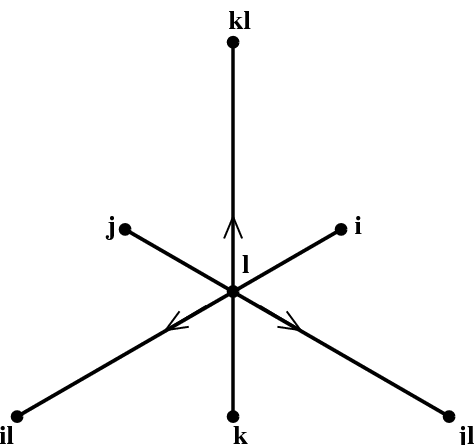
Figure 3: Three quaternionic subalgebras of $\OO$ which contain $\ell$.

We have so far been working with a particular quaternionic subalgebra. How many such subalgebras are there? We want to include our preferred complex unit, $\ell$, so that the reduction to 4 dimensions will work. So we are asking how many copies of $\HH$ are there in $\OO$ which contain a particular copy of $\CC$. If we add the reasonable requirement that any 2 such subalgebras intersect only in $\CC$, then there precisely 3 such subalgebras, labeled by $i$, $j$, and $k$, as shown in Figure 3. But there are precisely 3 generations of leptons!

The careful reader will have noticed that we have left out a massless particle, namely \begin{equation} \label{Oz} Ø_z=\begin{pmatrix}0\cr 1\cr\end{pmatrix} \end{equation} This particle is complex, and has the opposite helicity from the neutrinos $\nu$. As with the other massless states, this describes both a particle and an antiparticle. Alone among the particles, this one does not contain $k$, and hence does not depend on the choice of identification of a particular quaternionic subalgebra $\HH$ satisfying $\CC\subset\HH\subset\OO$.

We emphasize this basic asymmetry in the octonionic description of particles. In a a quaternionic description, we would have recovered the usual solutions of the Dirac description, namely a massive particle with 2 helicity states, and a massless particle with 2 helicity states. The fact that one helicity state is complex and the other quaternionic would seem to be simply a conventional choice. Over the octonions, however, there are 3 massive particles, each with 2 helicity states, 3 massless particles with just one helicity state, and a single, complex massless state with the opposite helicity; there are more massless particles of one helicity than the other.

In conclusion, there is room in this octonionic description for precisely the right number of leptons: exactly 3 generations, each containing massless particles having only a single helicity. These 2 properties, observed in nature, have yet to be explained theoretically.

But what about the extra particle, the $Ø_z$? In the picture presented here, it has no generation structure. The other neutrinos are hard enough to detect; it does not seem unreasonable to predict that this “sterile neutrino” would interact weakly if at all with ordinary matter. Is this dark matter?!