What happens if we add another, independent, square root of $-1$? Call it $\ell$. Here we go again.

In analogy to the previous construction of $\CC$ and $\HH$, an octonion $x$ can be thought of as a pair of quaternions, $(x_\Hone,x_\Htwo)$, so that \begin{equation} \OO = \HH \oplus \HH \, \ell \end{equation} Since we are running out of letters, we will denote $i$ times $\ell$ simply as $i\ell$, and similarly with $j$ and $k$. But what about the remaining products?

Of course, $\ell^2=-1$; this is built into the construction. It is easy to see that $i\ell$, $j\ell$, and $k\ell$ also square to $-1$; there are now 7 independent imaginary units, and we could write \begin{equation} x = x_1 + x_2 i + x_3 j + x_4 k + x_5 k\ell + x_6 j\ell + x_7 i\ell + x_8 \ell \label{xdef} \end{equation} where $x_m\in\RR$, which can be thought of as a point or vector in $\RR^8$. The real part of $x$ is just $x_1$; the imaginary part of $x$ is everything else. Algebraically, we could define \begin{align} \Re(x) &= \frac12 (x+\bar{x}) \\ \Im(x) &= \frac12 (x-\bar{x}) \end{align} where it is important to note that the imaginary part is, well, imaginary. This differs slightly from the standard usage of these terms for complex numbers, where “$\Im(z)$” normally refers to a real number, the coefficient of $i$. This convention is not possible here, since the imaginary part has 7 degrees of freedom, and can be thought of as a vector in $\RR^7$.

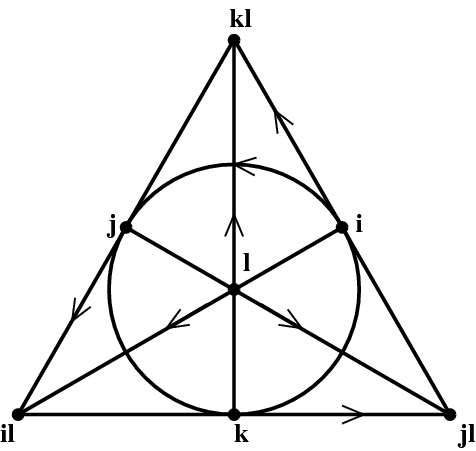
The full multiplication table is summarized in Figure 2. Each point corresponds to an imaginary unit. Each line corresponds to a quaternionic triple, much like $\{i,j,k\}$, with the arrow giving the orientation. For example, \begin{align} k \ell &= k\ell \\ \ell k\ell &= k \\ k\ell k &= \ell \end{align} and each of these products anticommutes, that is, reversing the order contributes a minus sign.

 
Figure 2: The octonionic multiplication table.