The complete classification of Lie algebras is one of the major results in mathematics, providing a description of the building blocks of all continuous symmetry groups. This classification was first outlined by the German mathematician Wilhelm Killing in the late 1800s, and the first rigorous construction was provided by French mathematician Élie Cartan shortly thereafter; both Killing and Cartan worked with complex Lie algebras.

We consider here only simple Lie algebras, namely Lie algebras which contain no nontrivial ideals. We also treat the abelian Lie algebra $\so(2)$ as a special case, which is isomorphic as a vector space to $\RR$, and in which all commutators vanish. 1) An ideal $\hh$ of a Lie algebra $\gg$ is a subalgebra of $\gg$ with the property that all commutators in $\gg$ involving one element of $\hh$ yield another element of $\hh$, that is, for which \begin{equation} X\in\hh,Y\in\gg \Longrightarrow [X,Y]\in\hh \end{equation} The zero set $\{0\}$ and the entire Lie algebra $\gg$ are both ideals of $\gg$; a simple Lie algebra has no other ideals. Roughly speaking, this means that any proper subalgebra of $\gg$ also mixes up the remaining elements of $\gg$ with each other.

The classification of simple Lie algebras proceeds roughly as follows. First, construct the largest possible subalgebra $\hh$ of $\gg$ such that all elements of $\hh$ commute with each other. There are many ways to do this, but $r=|\hh|$ is the same in each case, and is called the rank of the Lie algebra, while $\hh$ itself is called a Cartan subalgebra of $\gg$. Now fix a basis of $\hh$, and consider the action of these $|\hh|$ elements on (the rest of) $\gg$. Since our basis elements commute, we can find simultaneous eigenvectors for them (this is why the classification is done over $\CC$ rather than $\RR$), and it turns out that we can find a basis of $\gg-\hh$ that consists entirely of simultaneous eigenvectors. The corresponding eigenvalues are vectors in $\RR^r$, called the root system of $\gg$. The geometry of root systems turns out to be tightly constrained, and can be used to completely classify all simple Lie algebras.

This process sounds harder than it is in practice, so we give an example. We already know from § 10.2, that a basis for the Lie algebra $\su(2)$ is $\{\tau_x,\tau_y,\tau_z\}$, none of which commute with each other. Any Cartan subalgebra $\hh$ will therefore be 1-dimensional, so we pick $\hh=\langle\tau_z\rangle$, the 1-dimensional vector space with basis $\{\tau_z\}$. The (complex) eigenvectors of $\tau_z$ are \begin{equation} [\tau_z,i\tau_x \mp \tau_y] = i\tau_y \pm \tau_x = \mp i (i\tau_x \mp \tau_y) \end{equation} The reader who is familiar with quantum mechanics may recognize \begin{equation} L_z = i\hbar\tau_z = \frac{\hbar}{2}\sigma_z \end{equation} as the quantum operator corresponding to (the $z$-component of) spin, and \begin{equation} L_\pm = i\hbar \left( \tau_x\mp\tau_y \right) = \frac{\hbar}{2} \left( \sigma_x \pm i\sigma_y \right) \end{equation} as the corresponding raising and lowering operators. The classification of simple Lie algebras extends this construction to all (simple) symmetry groups — and works with anti-Hermitian matrices, rather than Hermitian matrices.

The geometric properties of root systems divide them into four infinite families, labeled $\aa_r$, $\bb_r$, $\cc_r$, and $\dd_r$, where $r$ is the rank, as well as five remaining cases, labeled $\gg_2$, $\ff_4$, $\ee_6$, $\ee_7$, and $\ee_8$; these latter five algebras are referred to as the exceptional Lie algebras. It turns out that \begin{align} \aa_r &\cong \su(r+1) &(r\ge1)\\ \bb_r &\cong \so(2r+1) &(r>1)\\ \cc_r &\cong \sp(r) &(r\ge3)\\ \dd_r &\cong \so(2r) &(r\ge4) \end{align} where the restrictions on the rank are to prevent overlaps, since \begin{align} \aa_1 &\cong \bb_1 \cong \cc_1 \\ \bb_2 &\cong \cc_2 \\ \aa_3 &\cong \dd_3 \end{align} and $\dd_1\cong\so(2)\cong\RR$ and $\dd_2\cong\so(4)\cong\so(2)\oplus\so(2)$ are not simple.

The root diagrams for the rank 2 Lie algebras $\aa_2$, $\bb_2$, $\dd_2$, and $\gg_2$ are shown in Figure 1. Each arrow represents a root; there are $|\gg|-|\hh|$ roots in all, since the Cartan elements are not included. The overall scale is a matter of convention, but the relative scale within each diagram is not. Further discussion of the construction of root diagrams can be found in [Wangberg and Dray] .

Comparing the list of simple Lie algebras and their corresponding Lie groups with our previous results, we see that the $\aa$ family corresponds to the unitary groups $\SU(n)=\SU(n,\CC)$, the $\bb$ and $\dd$ families together correspond to the orthogonal groups $\SO(n)=\SU(n,\RR)$, and the $\cc$ family corresponds to the symplectic groups $\Sp(n)=\SU(n,\HH)$. Do the remaining, exceptional Lie algebras correspond to Lie groups over the octonions? Yes, indeed! We will return to this discussion in § 11.

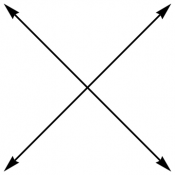
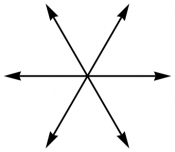
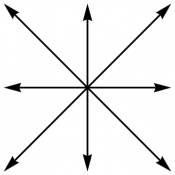
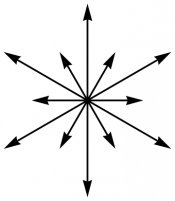Figure 1: The root diagrams for $\dd_2=\so(4)$, $\aa_2=\su(3)$, $\bb_2=\so(5)$, and $\gg_2$, respectively.